直角二等辺三角形の辺の長さ 直角二等辺三角形の辺の長さの割合は1対1対ルート2です。 これがよくわかりません・・・ もう少し詳しく教えて欲しいです。 お願いしますm(_ _)m よろしくおねがいします。黄金三角形の定義と正五角形 黄金三角形の定義 黄金三角形とは,長い2辺と短い辺が黄金比になっているような二等辺三角形のことです.黄金比とは,$1\phi$ のことです.側面の二等辺三角形の底辺の長さと高さの比 ピラミッドのしゃめんの長さと底面の半分の長さの比 ピラミッドについてご覧になりたい方は⇒ピラミッドHP ギリシャのパルテノンしんでんにかくされてい

二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学
平行四辺形 相似 三角形 面積比
平行四辺形 相似 三角形 面積比- 11√2の45度直角二等辺三角形の辺の比率を利用して、先ほどの式で高さ部分を求めることができます。 難しい感じた方でも大丈夫。「d ≒07」さえ覚えておけば、例ば「c5」のときは、 d×5 ≒35というふうに、倍にすることでどの場合でも簡単に求められ この時に三角関数の比率を使って水平方向の力、鉛直方向の力を計算する事が可能です。 ここではsinθ、cosθなど難しい言葉は使わずに説明していきます。 直角二等辺三角形の形(90度と45度) 斜めの力が2とします。




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
2角が等しいので aceは二等辺三角形となる。よってae=ac(4) ad//ecよりbaae=bddc(5) (4),(5)よりabac=bddc 例adが∠bac の二等分線とする。二等辺三角形を見つけることができるので、それをたどっていくと、\(AB=x1\) と表せますね。 これを用いて相似比をとっていくと、次のように \(x\) を求めることができます。 二等辺三角形の面積Sとその底辺bがわかっている場合は、三角形の面積S = b * h / 2を求める公式から、高さhを求めます。 h= 2 * S / b。 底辺bまで下がったこの高さは、与えられた二等辺三角形を2つの等しい直角三角形に分割します。
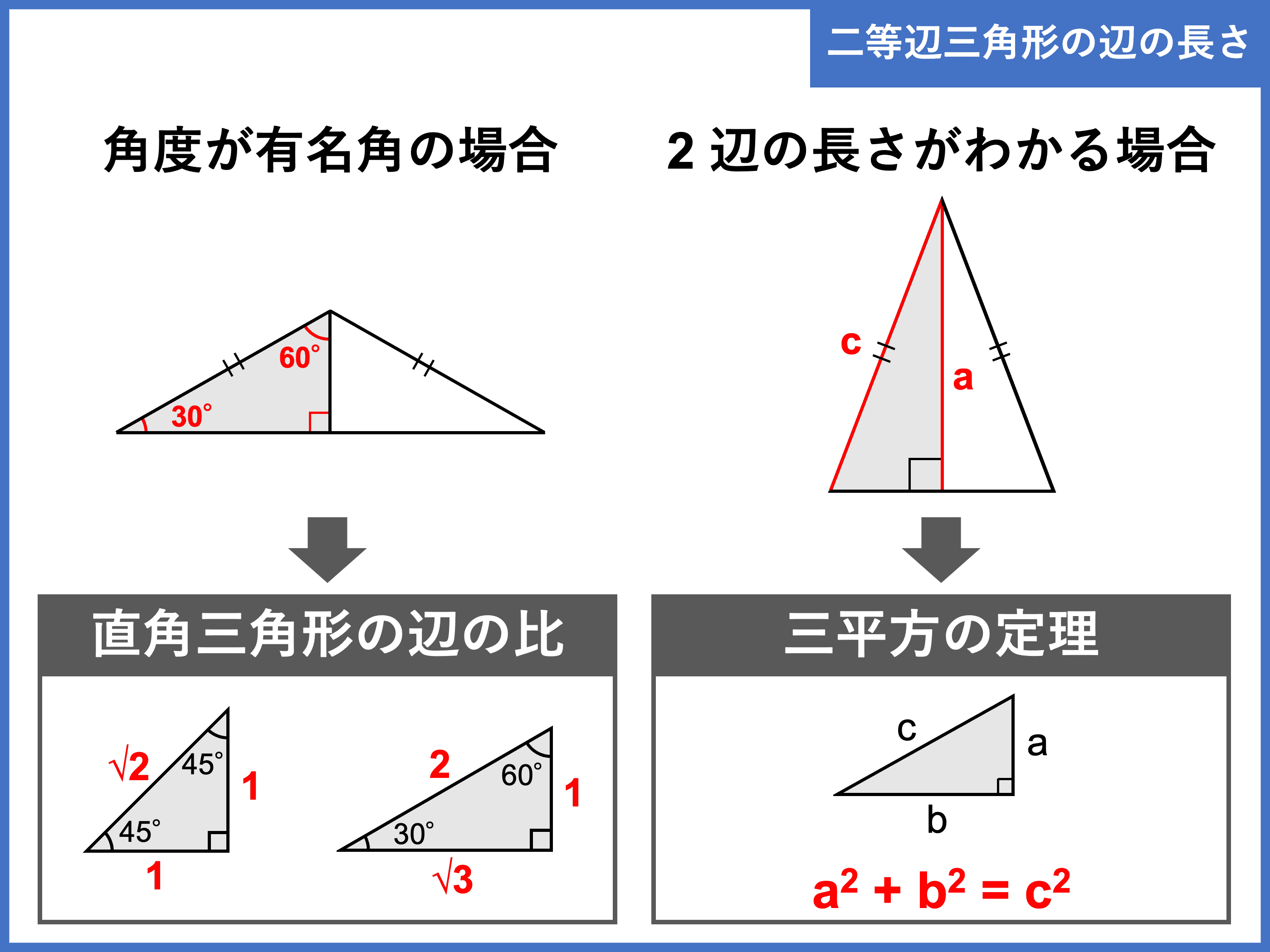
直角二等辺三角形の底辺と高さの長さは同じです。 底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。 よって、直角二等辺三角形の辺の比は「1:1;√2」です。 今回は、直角正三角形とは3つの辺の長さが等しく、3つの角の大きさが等しい形のことです。 これが 二等辺三角形(にとうへんさんかくけい) です。 二等辺三角形とは、 2つの辺の長さが等しく、2つの角の大きさが等しい形 のことです。 一方で白銀比には、別名 大和比と第2貴金属比の 二種類 があります。 このうち 大和比は、日本古来の建築や彫刻 に用いられてきた比率 数学的には√2。学校で習った「 一夜一夜に人見頃()」です。 直角二等辺三角形の辺の比に相当します。
二 等辺 三角形 比率 適切な 二 等辺 三角形 比率 壁紙 配布 各辺の比が決まっている三角形 / 中学数学 by OK 直角二等辺三角形のそれぞれの辺の比率は11√2 直角二等辺三角形とは?定義や辺の長さの比、面 二等辺三角形とは?第233問 直角二等辺の辺の比 図形ドリル 直角三角形 直角二等辺三角形 相似 ★★★★★☆(算オリ・灘中受験生レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな学習する学年:中学生 1.三角比って何? 三角比とは、直角三角形の3つある角の90度以外のどちらか1つの角度が決まれば、3つの辺の長さの比率が決まるという性質のことです。 注意:直角二等辺三角形の場合は角度が決まらなくても3辺の比率は決まってしまいます。




15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext




36 72 などの三角比 数学i フリー教材開発コミュニティ Ftext
黄金三角形(おうごんさんかくけい)は、長い2辺と短い辺の長さの比 が黄金比 = になっている二等辺三角形である。 黄金三角形は、大星型十二面体や小星型十二面体の展開図に現われる。 また、対角線を引いた正五角形や正十角形の中にも見出すことができる。直角二等辺三角形です。 関連: 直角二等辺三角形の辺の長さの求め方 サインは (遠い辺) / (斜辺) なので、$\dfrac{1}{\sqrt{2}}$ となります。バージョン PhotoShop22(2311) 今回は 三角形 (正三角形、二等辺三角形)と色,太さ,塗り,点線,外枠線,サイズ変更の作成方法を解説していきたいと思います。 それでは行ってみましょう!




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube



2つの相似な二等辺三角形が図のように1辺を共有しています Aとdはそれぞれ着色された領域です A D 9 が成立するときの Cos A の値は Quora
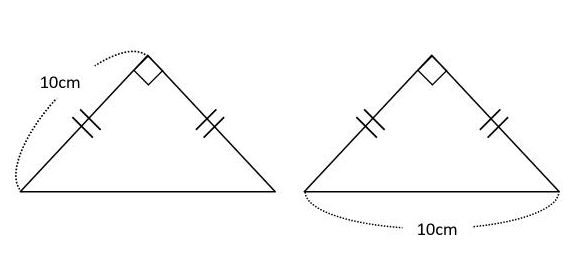
4vで使用する三角形は5種類あります。各三角形で使用するフレームは3本ですが、実際には正三角形は1種類、二等辺三角形は2種類、さらに隣り合わせで共用部分があるので aab は2種類 bcc は21(既出bを引く)=1 cdf は31=2(既出cを引く) 二等辺三角形の一辺から 直角に線 を引き、 高さ を作ります。 高さの長さを求める 補助線により出来た三角形は、 30°, 60°, 90°の直角三角形 です。 この 三角形は 一番長い辺と一番短い辺の 長さの比が 2 1 になっています。 ※ 30°, 60°, 90°の三角形(三角定規)の長さの比 は 覚えてお図のような二等辺三角形のa点に荷重 10n が加えられたときの、各部材に発生する力を求めます。 a点に 10n の荷重が働くとき、このトラス構造は二等辺三角形であるため、b点、c点に働く 反力 r b , r c はそれぞれ 5n となります。




二等辺三角形の面積を求める算数の公式は




くろべえ 18 36 54 72 の三角比 Sin Cos
・ 1:2:2 二等辺三角形で,頂角が約29° 精度を求めなければ,日常的には,正三角形の二等分線を作るより楽です。 ・ 2:2:3 二等辺三角形で,頂角約97°,底角約41° ・ 2:3:4 約104°,約47°,約29° 解説 まず、二等辺三角形がたくさん見つかることがわかるよね! だから、二等辺三角形の特徴である " 2 2 角が等しい" を利用してみるよ。 すると、こんな風に文字を置けるね! はい、カラフルになりました。 ここからどうすればいいかわかるかな 直角二等辺三角形で、二等辺が、16cmです。その場合、「斜辺」は、何センチになるでしょうか?よろしくお願いします。 数学 解決済 教えて!goo




15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext



3 4 5の三角形で 本当に直角ができる Note Board
まとめ:二等辺三角形の底辺は二等分線からはじまる。 二等辺三角形の底辺の計算は簡単。 頂角の二等分線を底辺にひく 底辺の半分の長さを求める そいつを2倍する っていう3ステップでいいんだ。 どんどん問題をといてみよう! そんじゃねー Ken こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がか辺の長さの比1:1:1 直角二等辺三角形です。 直角をはさむ2辺の長さは同じ です。 辺の長さの比1:1:√2 60°と30°の直角三角形です。 いちばん長い辺はいちばん短い辺の2倍の長さ です。 辺の長さの比1:2:√3 3辺の比が簡単な整数となる直角




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月



相似比と底辺比から面積比を求める 基準となる三角形を探せ みみずく戦略室
まずこの二等辺三角形の配置が有名配置であることを 知っておきたいです。 二等辺三角形 \(dca\) の外角 と 二等辺三角形 \(cdb\) の内角より 角の大きさは下図のようになります。 さらに、\(ab=ac\) という条件もあるので、 三角形 \(abc\) は二等辺三角形です。円を二等辺三角形に変形させる方法を紹介します。 まず、芯がなく、中に空洞がない "トイレットペーパー" の側面を想像してください。これを上から中心に向かって切断して中を開きます。 では、なぜ内角の二等分線と比にはこのような性質があるのか証明してみましょう。 まず、辺 と平行な線を点 を通るように引きます。 すると、図のように同位角、錯角により が二等辺三角形になることが分かります、 つまり、 となります。 最後に




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学
直角二等辺三角形(ちょっかくにとうへんさんかくけい、英 isosceles right triangle )は、二等辺三角形の持つ特徴に加え、直角三角形の持つ特徴を併せ持つ図形である。 3つの角のうち2つの角がそれぞれ45°である三角形と定義してもよい。 直角二等辺三角形は二等辺三角形の一つでもあり、直角$15^\circ$ の三角比の値は覚えなくてもよいが、$15^\circ$ を含む直角三角形から導けるようにしておこう。 これらの角以外にも、$18^\circ$、$36^\circ$、$72^\circ$、$144^\circ$ などの角も、特殊な三角形を考えることによって三角比を 求めることができる。送信を完了しました。 直角二等辺三角形 のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 小・中学生 高校・専門・大学生・大学院生 主婦 会社員・公務員 自営業 エンジニア 教師・研究員 その他 この計算式は 非常に




三角比 30 45 60 もう一度やり直しの算数 数学




三平方の定理と二等辺三角形 Youtube
二等辺三角形の高さの求め方は下記をご覧ください。 二等辺三角形の高さの求め方は?3分でわかる計算、辺の長さ、角度との関係、30度の高さ 二等辺三角形の底辺と三平方の定理の関係 二等辺三角形の底辺の長さは、三平方の定理でも計算可能です。まずは、 三角形 その後、我々は両方の分類を組み合わせるというように急性二等辺三角形、急性不等辺、右斜角筋を含むいくつかの他の結果を得ることができます。 スライドでは、あなたが三角形を描くときに、Shiftキーは、各辺の比率を維持します 直角二等辺三角形だと この公式。 と別々に覚えるのは大変ですね。 ですので、やみくもに公式を覚えるのではなく、 (底辺) × (高さ) ÷ 2 が当てはまる、 底辺 と 高さ を探す ほうが、簡単 だと思います。 三角形の面積公式が (底辺) × (高さ) ÷ 2 となる




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




スタディピア 図形




スタディピア 図形




白銀比三角形を見ていて気付いたこと 大したことない Yoshidanobuo S Diaryー高校数学の 思考 判断 表現力 を磨こう ー




三角比15ºと75º 数式で独楽する




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




15度直角三角形の斜辺の長さ Youtube




よく使う三角比の値 数学i By Okボーイ マナペディア
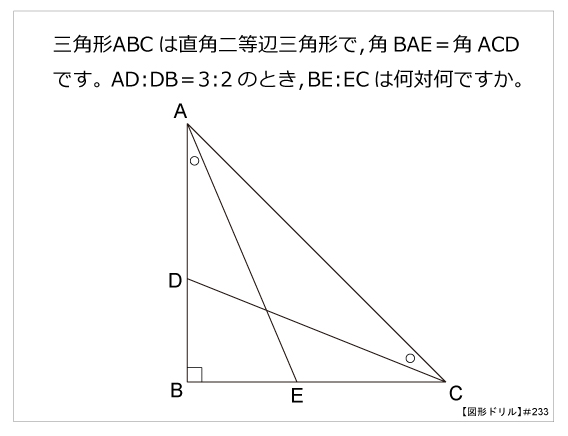



第233問 直角二等辺の辺の比 図形ドリル 第233問 直角二等辺の辺の比 算数星人のweb問題集 中学受験算数の問題に挑戦




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




三角定規の直角三角形のときは 比の計算で簡単に求めよう 中学や高校の数学の計算問題
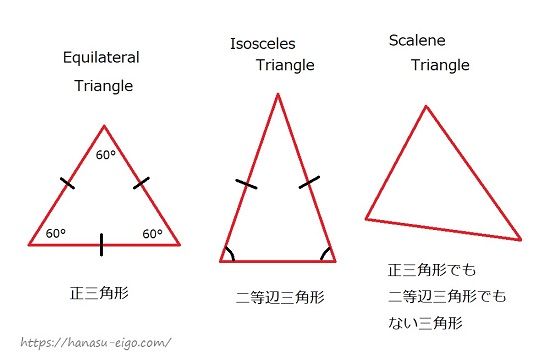



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語
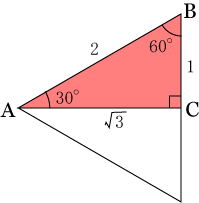



基本三角形と三角比



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
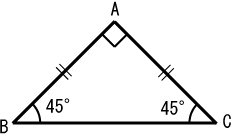



直角二等辺三角形 Wikipedia
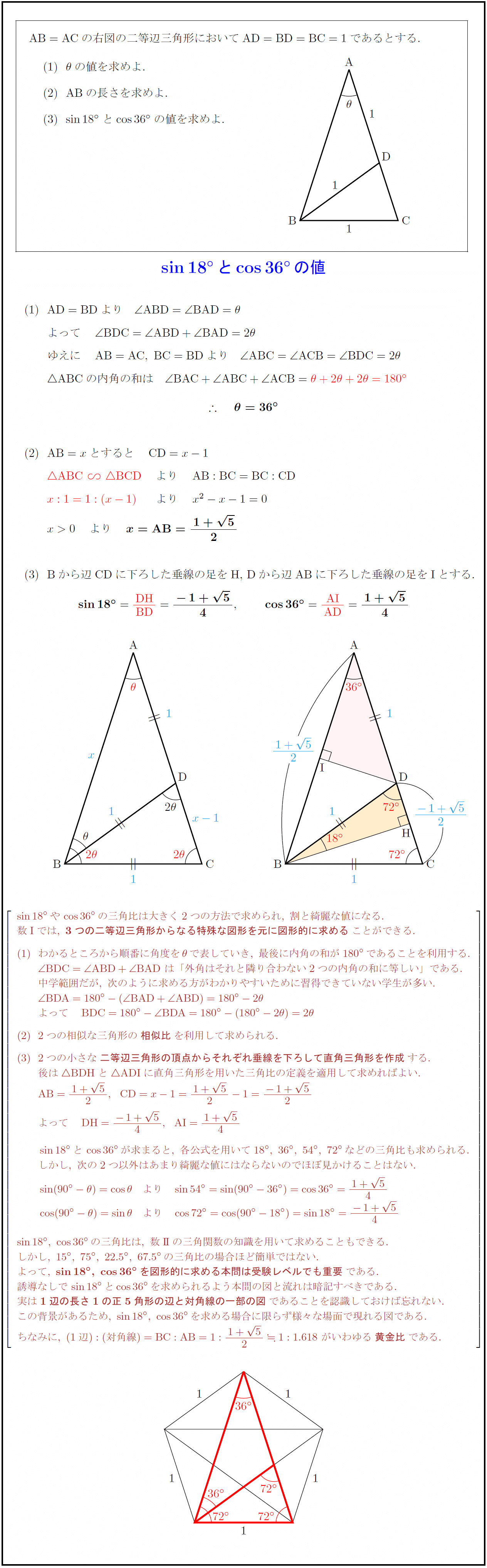



高校数学 Sin18 とcos36 の値 正五角形を利用した図形的解法 受験の月




応用 36度の三角比 なかけんの数学ノート
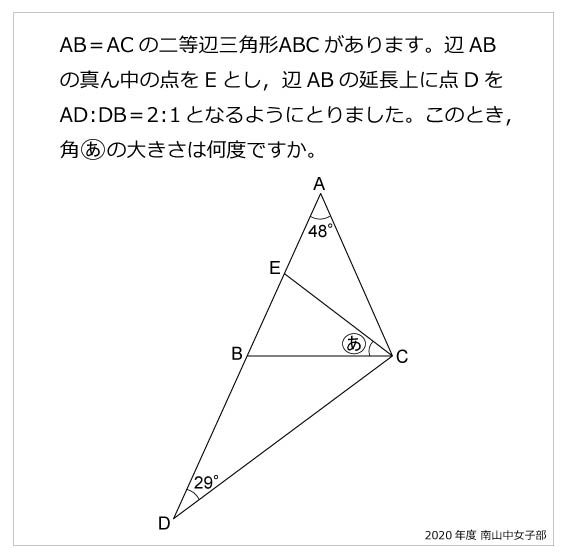



二等辺三角形 算数星人のweb問題集 中学受験算数の問題に挑戦
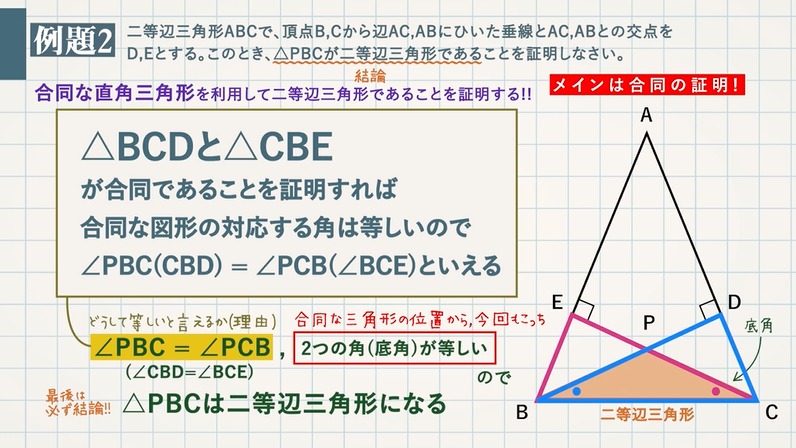



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
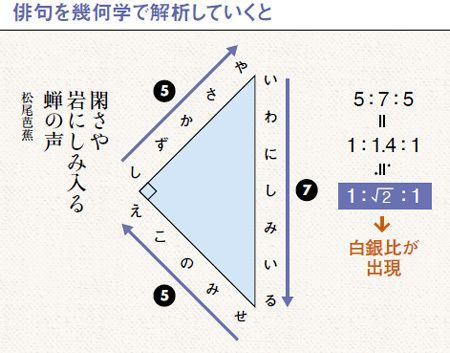



5 7 5 の俳句に隠されていた 白銀比 2ページ目 President Online プレジデントオンライン



2




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
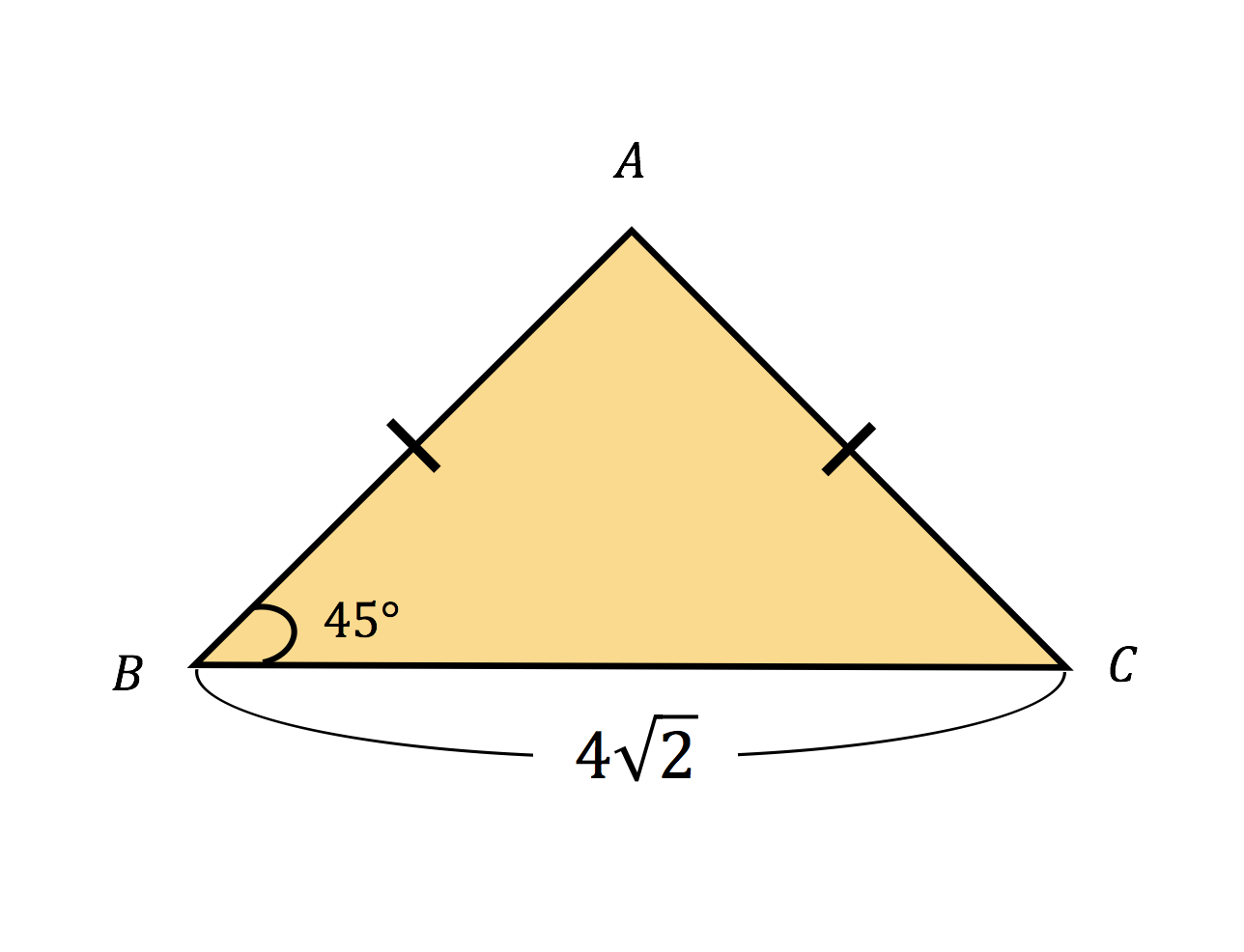



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




特別な直角三角形の辺の比 無料で使える中学学習プリント
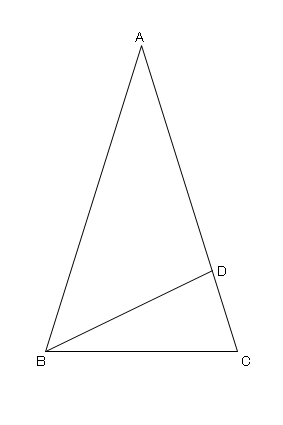



三角形の相似の証明 2 ネット塾
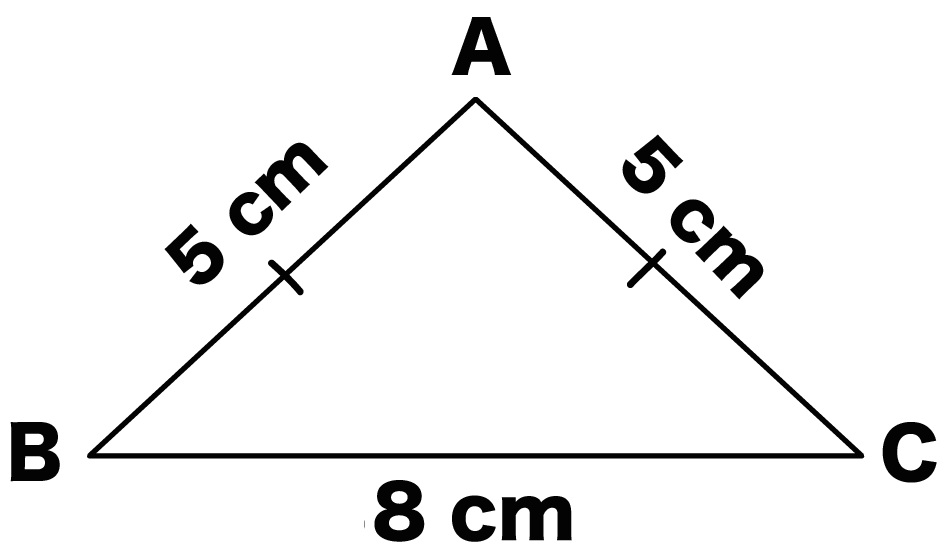



簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
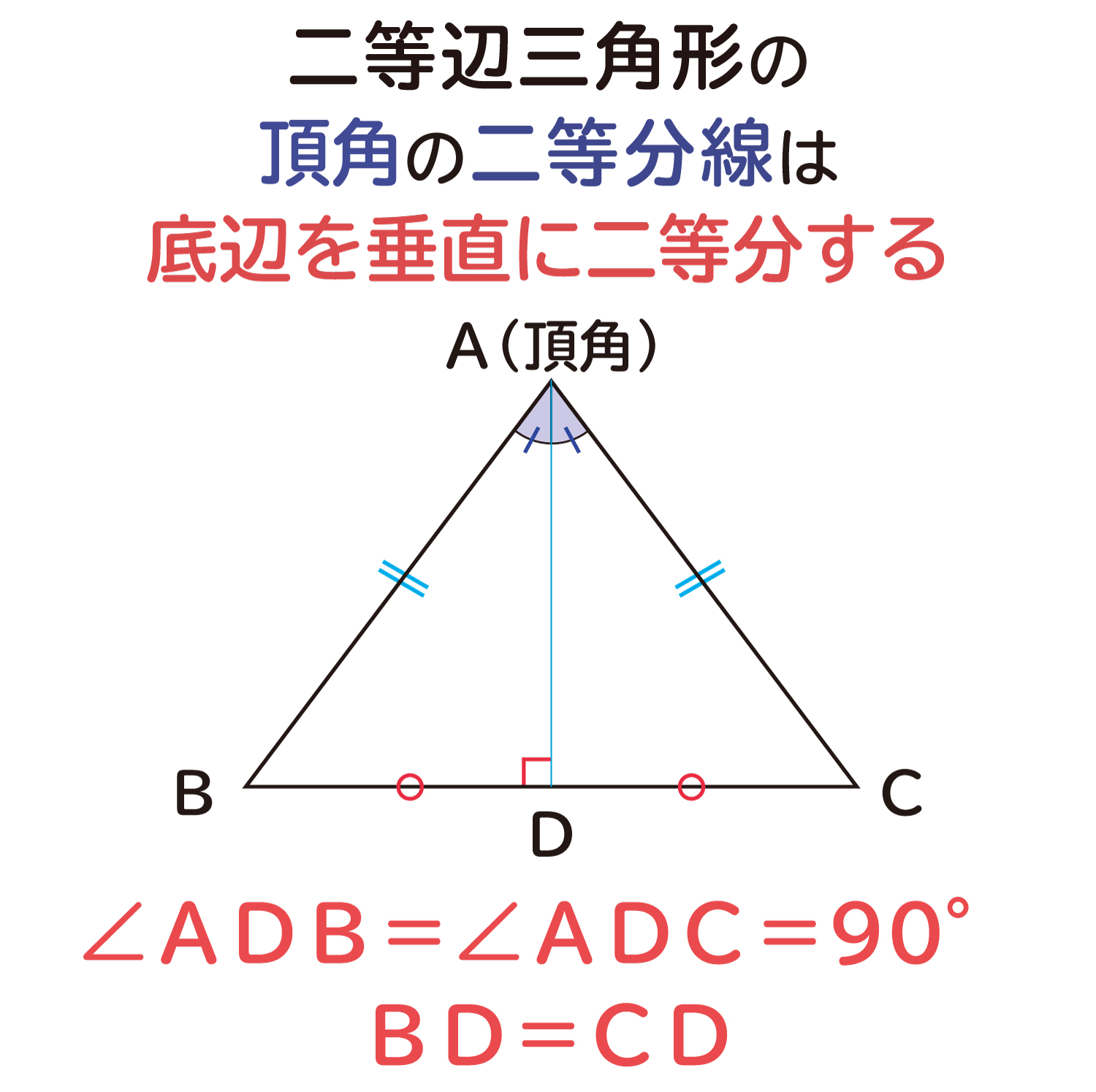



二等辺三角形の頂角の二等分線は 底辺を垂直に二等分する ことの説明 おかわりドリル
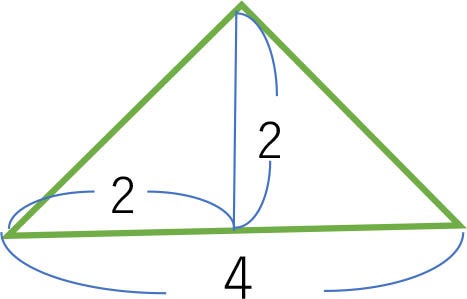



面積 直角二等辺三角形 小学4年生算数 そらいろ日記 言葉の宝箱




各辺の比が決まっている三角形 中学数学 By Okボーイ マナペディア




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




36 の三角比 二等辺三角形を用いて求める方法は Youtube



1




頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




36 72 などの三角比 数学i フリー教材開発コミュニティ Ftext



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明




今 二等辺三角形が熱い 小学校の算数が懐かしい デイリーポータルz
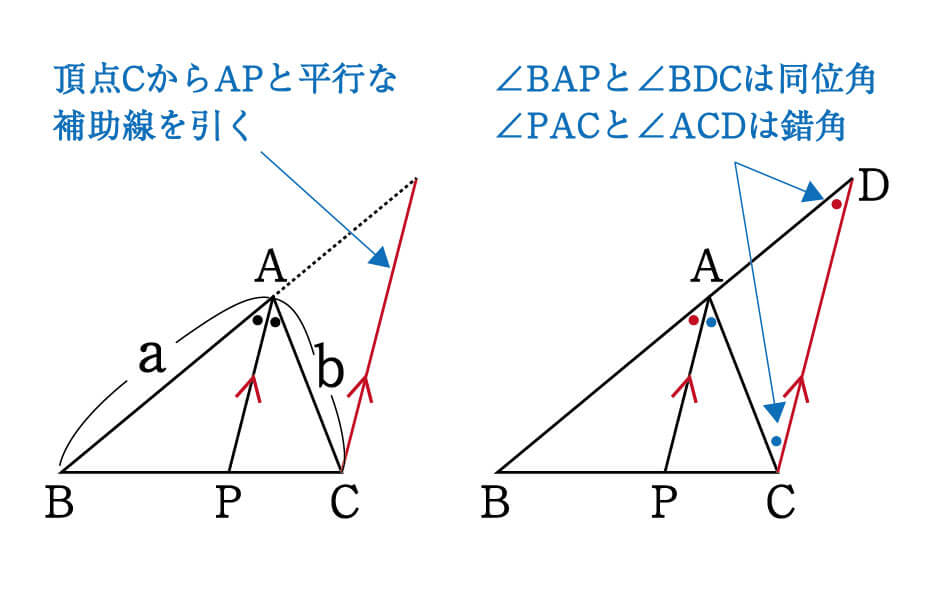



数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典



二等辺三角形の高さの求め方は 3分でわかる計算 辺の長さ 角度との関係 30度の高さ



1
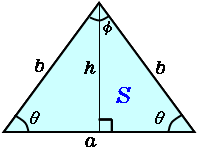



二等辺三角形 高精度計算サイト




直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう




この二等辺三角形の角度を求めてください この三角形は Ab Acの二等辺 Okwave




確認 三平方の定理 直角二等辺三角形 高校生 数学のノート Clearnote




二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題
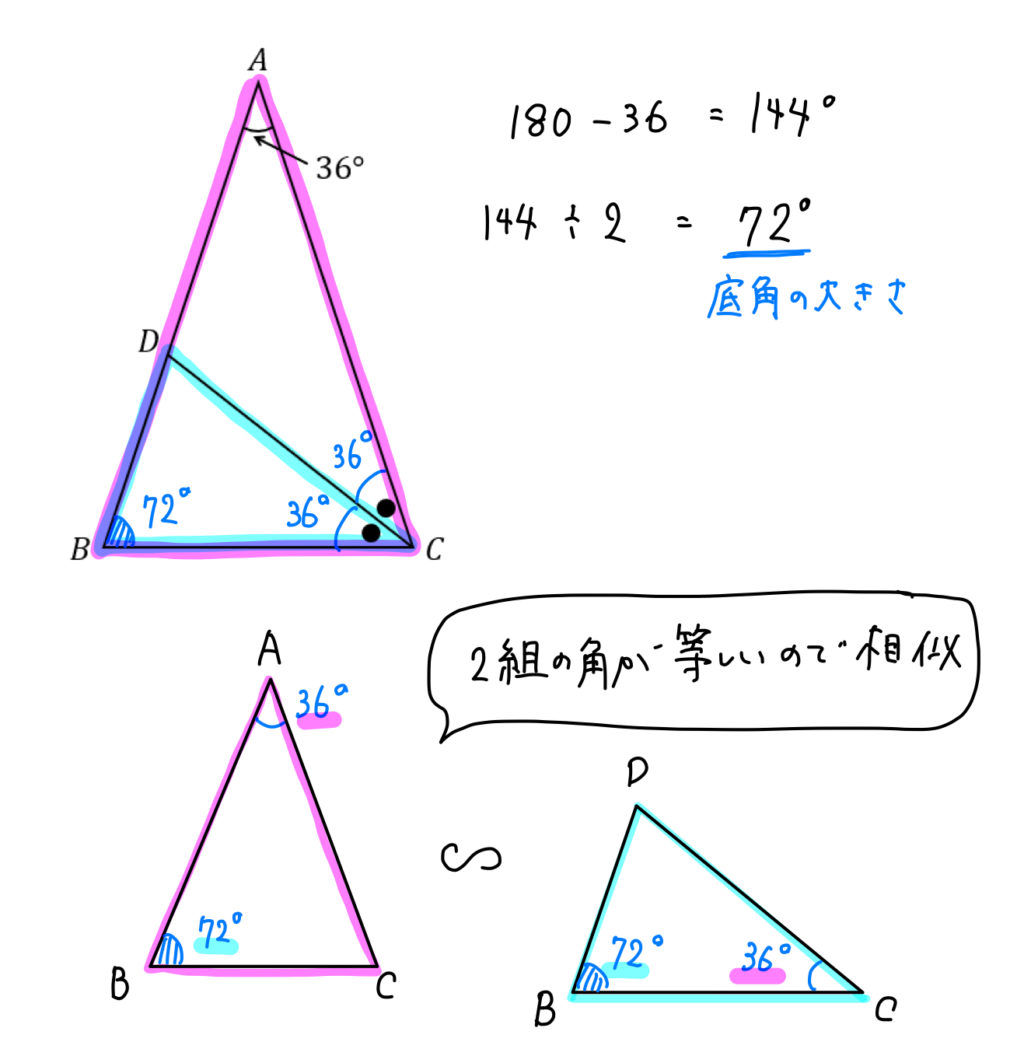



数学 36 の三角比 二等辺三角形を用いて求める方法は 数スタ




標準 ベクトルの内積と二等辺三角形 なかけんの数学ノート



直角二等辺三角形と三平方の定理の関係は 3分でわかる計算 公式 辺の比 例題




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット



連続する二等辺三角形の角度の法則 算数解法の極意
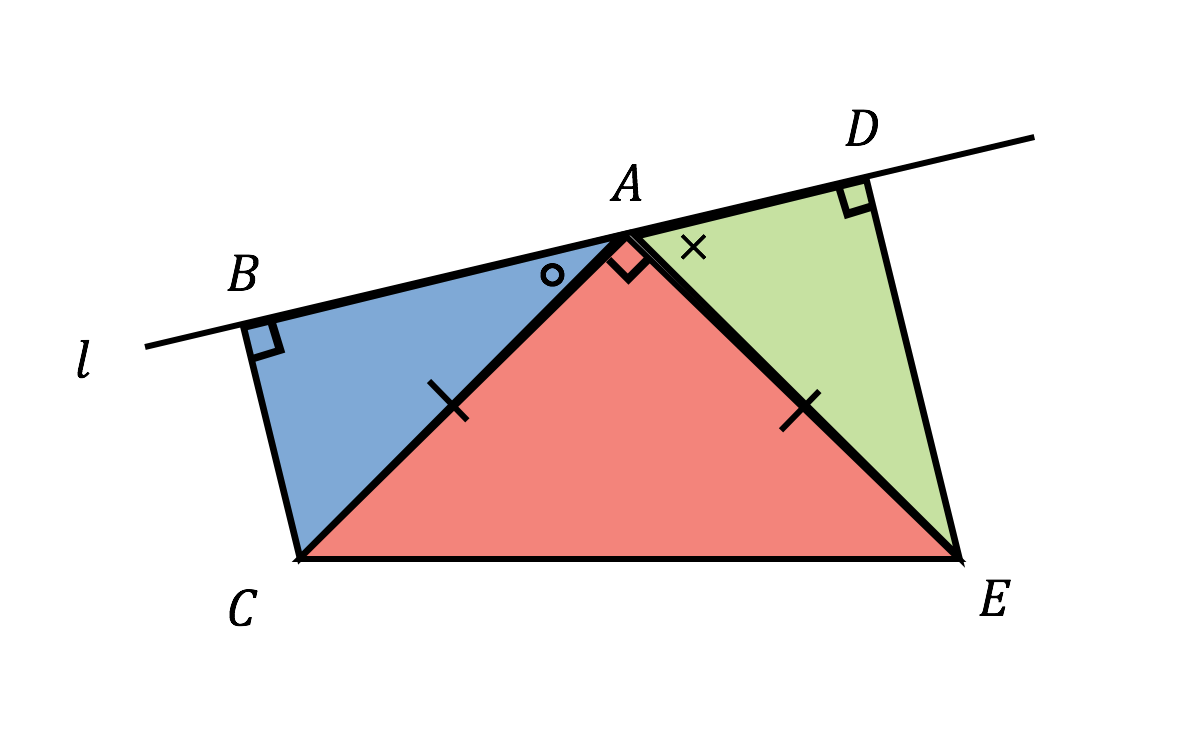



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ
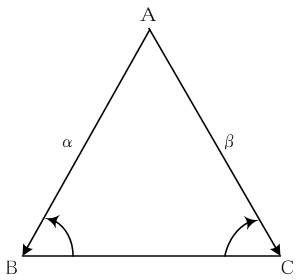



3 2 三角形とベクトル比




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理 覚えること 三角定規 苦手な数学を簡単に



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



二等辺三角形とは 定義 定理や 角度 辺 面積の求め方 受験辞典
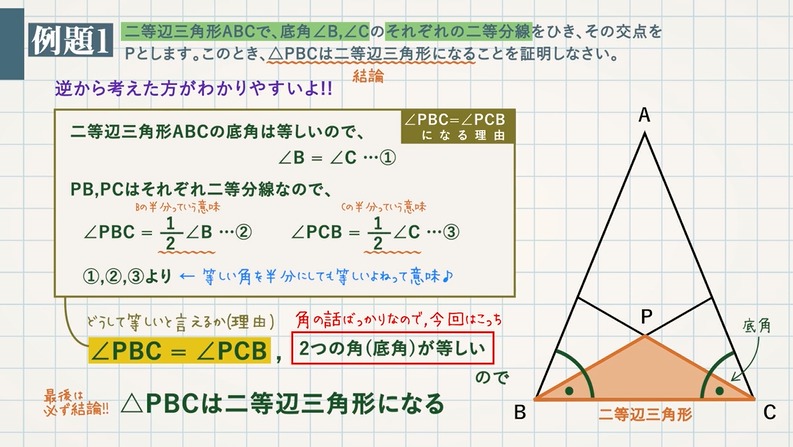



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




この公式は角度が1のときだけ使えるのですか Clearnote



1
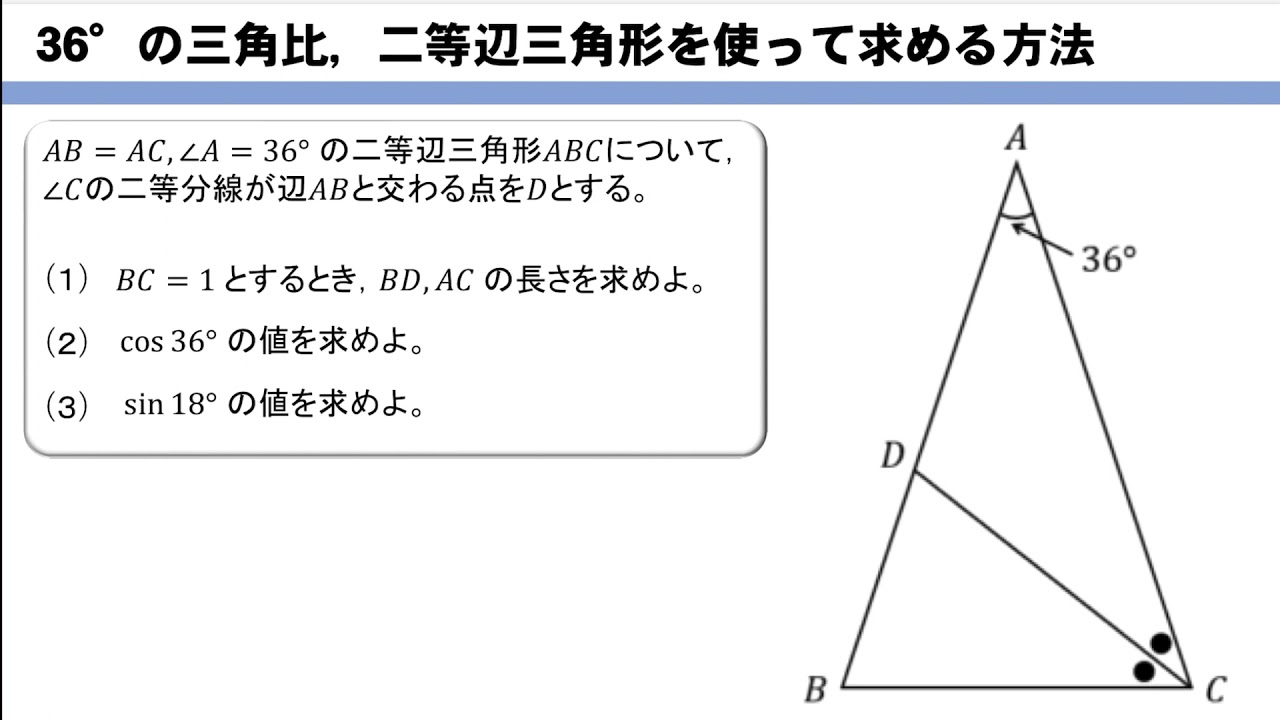



36 の三角比 二等辺三角形を用いて求める方法は Youtube




三角形の問題 平行 二等辺三角形 問題 三角形abcにおいて 角bの二 Okwave




勉強しよう数学0 三角比 2 tam15度
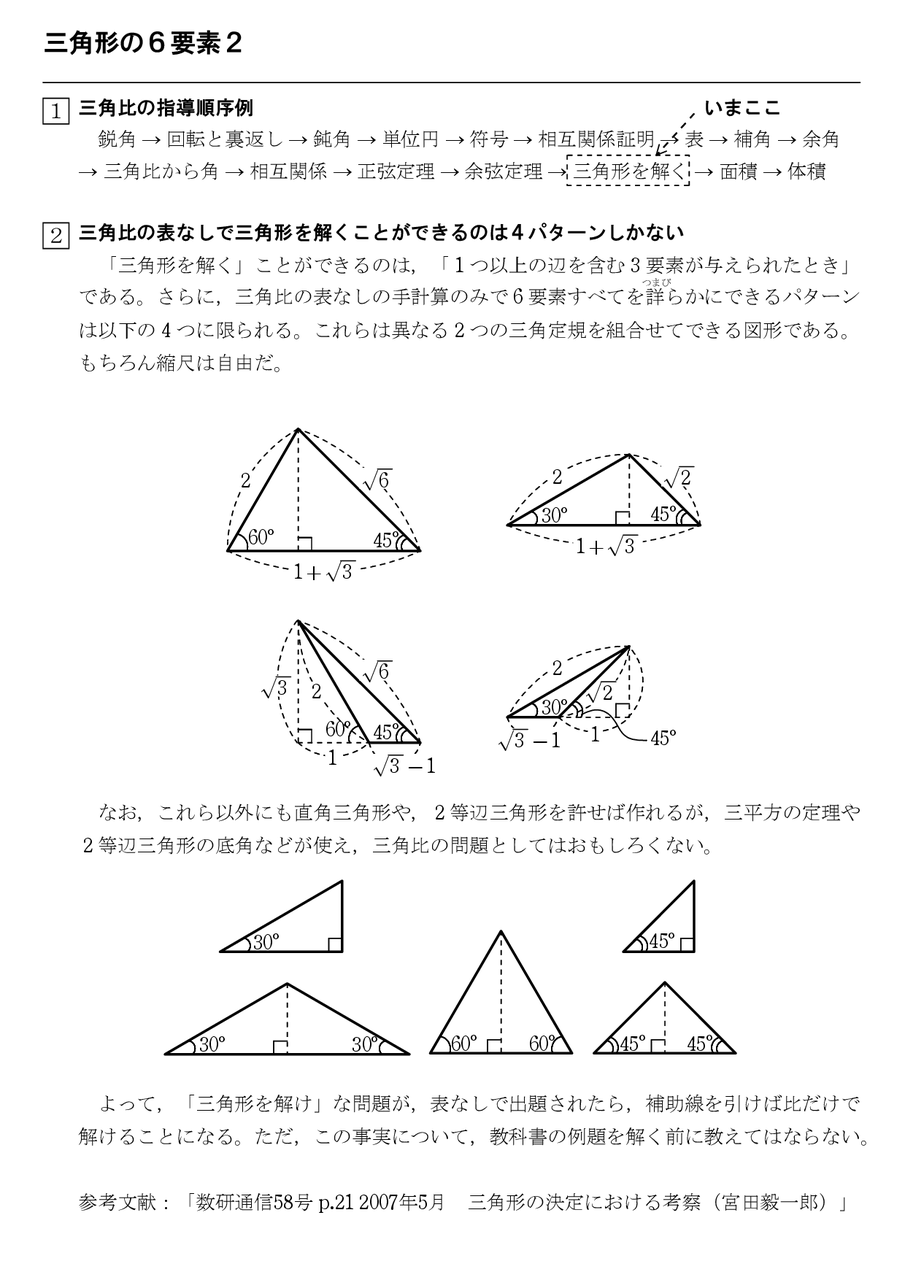



三角形の6要素2 怜悧玲瓏 高校数学を天空から俯瞰する




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




黄金三角形による18 シリーズの三角比 おいしい数学
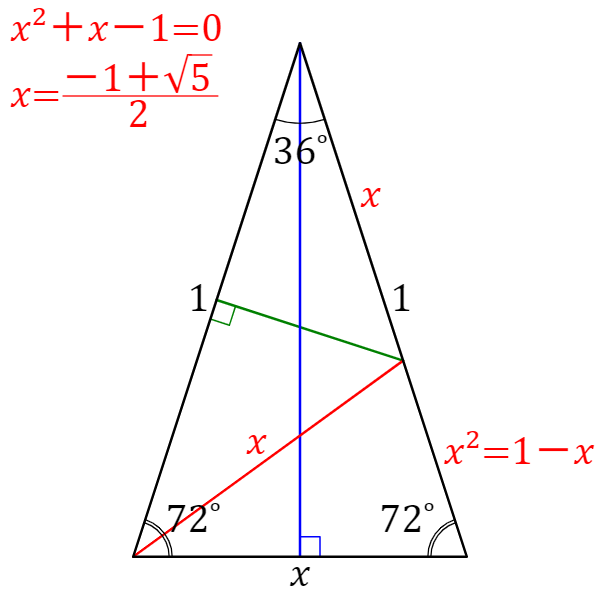



Sin18 Cos72 Cos36 Sin54 を簡単に求める方法 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




テストによく出る直角三角形の辺の比 中学数学 By じょばんに マナペディア
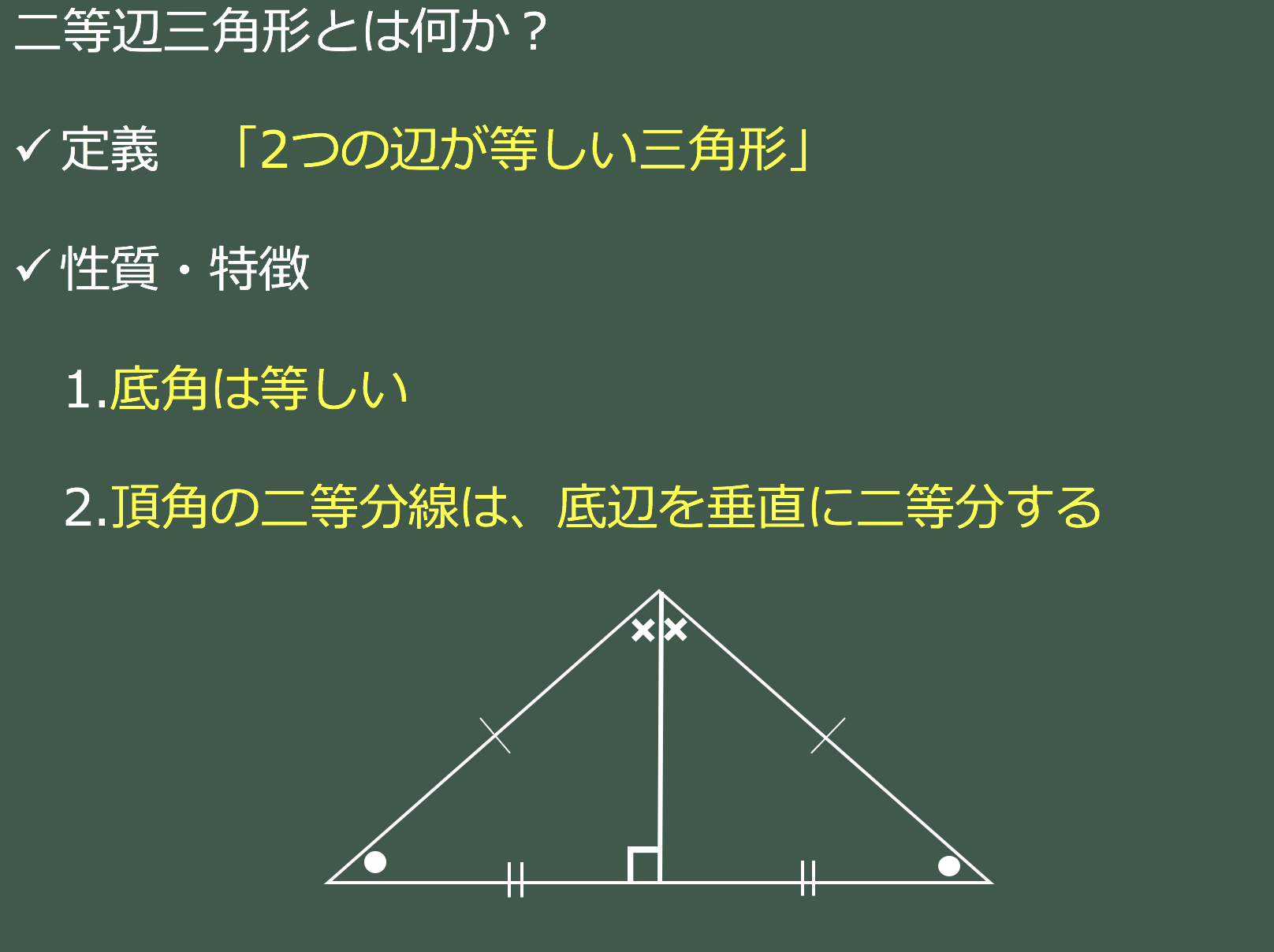



3分で分かる 二等辺三角形の特徴 角度 辺など についてわかりやすく 合格サプリ




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




特別な直角三角形の辺の比 無料で使える中学学習プリント




15 シリーズの三角比 おいしい数学
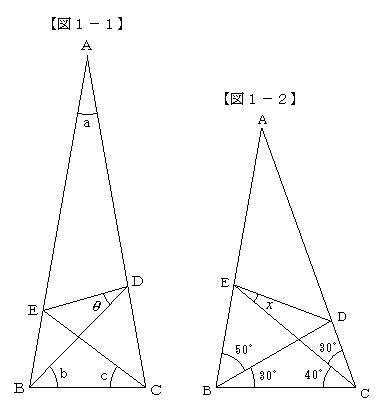



偶然の角 の一般化にむけて




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ



2



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明
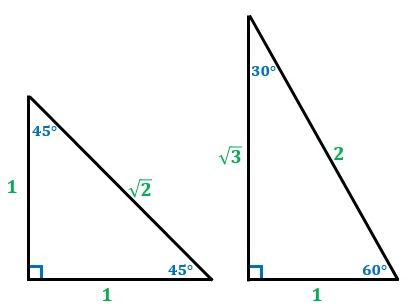



直角三角形の辺の比 東久留米 学習塾 塾長ブログ




三角関数とは Part1 三角比 Sin Cosとは Toy 数学 Note




三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア




スタディピア 図形



二等辺三角形の分割



3
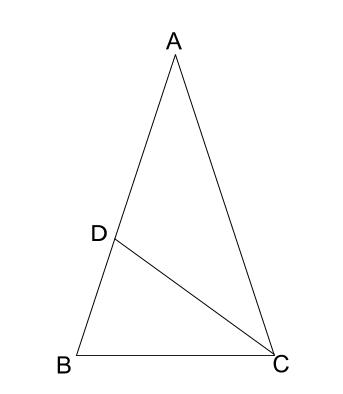



中学数学 相似と方程式 中学数学の無料オンライン学習サイトchu Su


