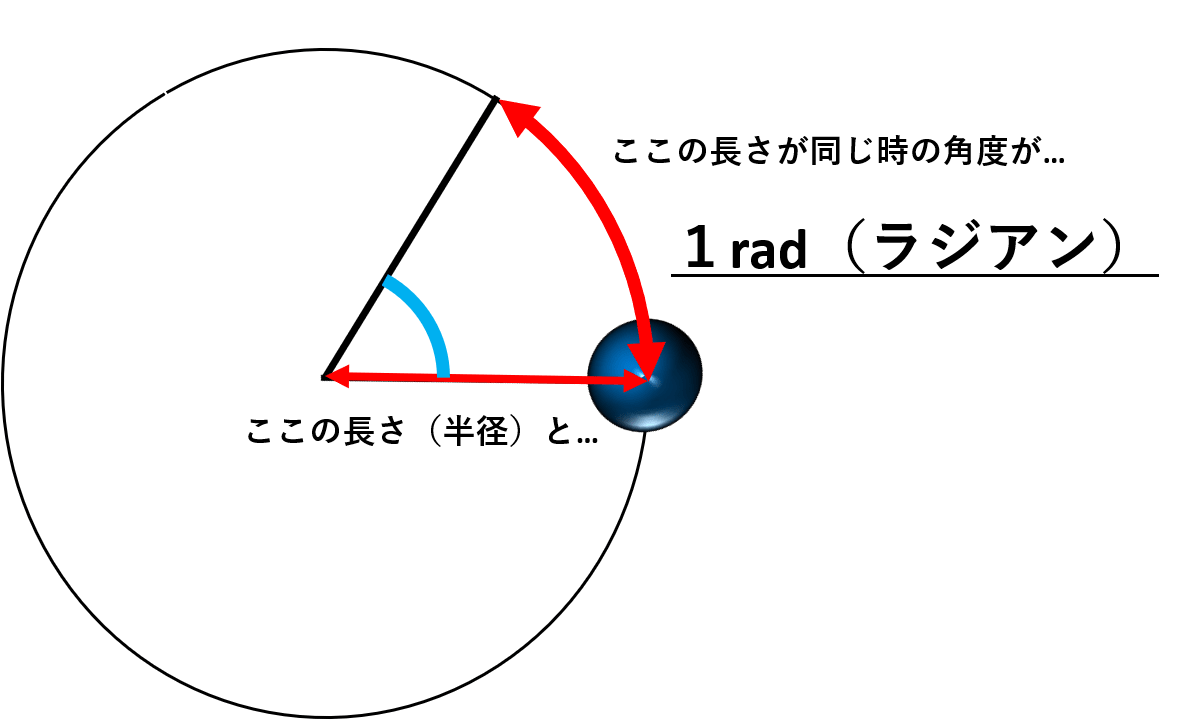
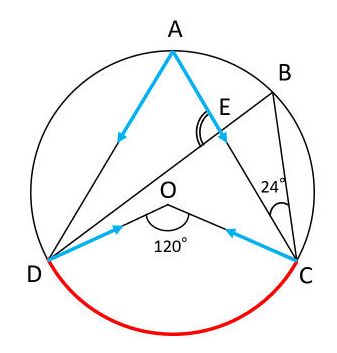
2 右図のように ∠ ACB の中に円 ただし, ∠ BOA は図のように,優角(180°よりも大きい角)の方とする 《問題》 次の角度 x , y , z を求め弧度(こど)とは、2本の半径および半径と同じ長さの弧が成す角度です。下図をみてください。αを弧度といいます。 弧度αの値を求めましょう。円弧の長さr、角度α、円周の長さ2πr、円の角度360°の関係は下記です。 r:2πr=α:360 r×360=2πrα円の弧長,弦長,矢高,半径のどれか2つを与えて残りを計算 実行数 (1)求めたい2つに"0"を入れる、空白にしない、ということをやられていない 本ライブラリは会員の方が作成した作品です。 内容について当サイトは一切関知しません。

おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook
円 角度 求め方
円 角度 求め方-円が描けてしまえば、図の幾何学的な関係から以下の式を簡単に導くことができます。 まずは円の半径を下式(5224)で求めます。 ・・・(5228) 主応力、主応力方向までの角度θは以下の式で求めることがでいます。A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 弓形 A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐
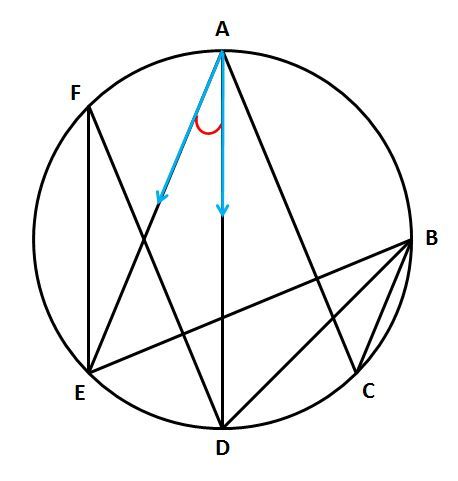


円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室
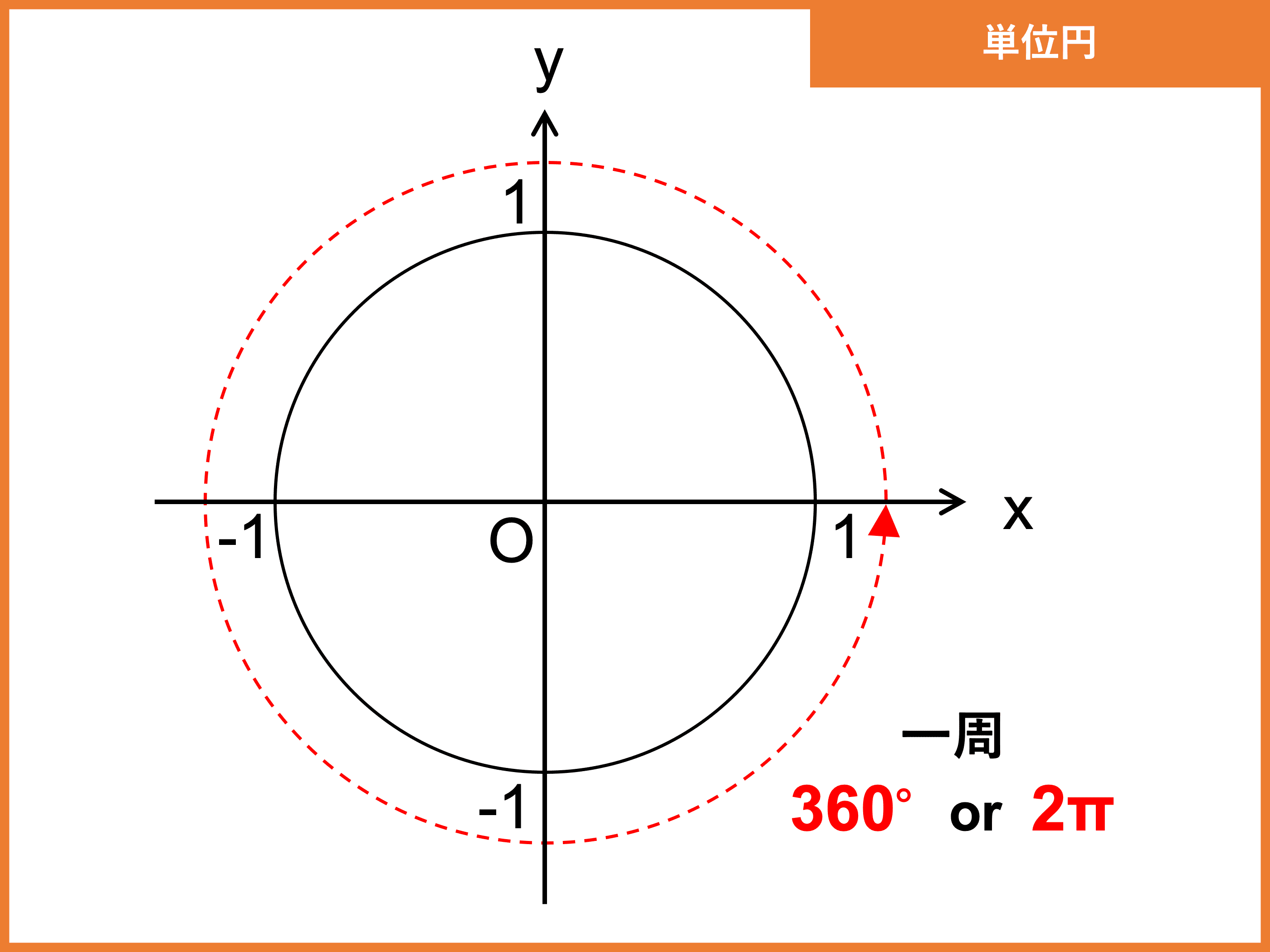
角xの角度を求めなさい。 → 解答 問題6 下の図の三角形ABCの辺ABは外接円の直径です。角Cの角度は何度ですか。 → 解答 問題7 下の図のOは円の中心です。∠x,∠yの大きさを求めなさい。 → 解答 問題8以上をまとめると三角方程式の解き方は「 単位円 を描き、 y=aの直線 を加えて、 三角形の比 を求めて角度を求め、 範囲を確認 して当てはまるもののみ答える」となります。 また、三角形の比は有名角のもの(30°、45°、60°など)に限られます。半径の求め方は? 半径は円の中心から端部までの距離です。下図をみてください。これが半径です。 円の性質を利用した半径の求め方は、いくつもあります。例えば、 直径=半径×2 の関係があります。直径とは円の中心を通る両端部間の距離です。
こんにちは。 da Vinch (@mathsouko_vinch)です。 三角関数においてある角度の三角比を「覚える」のはナンセンスです。なぜなら三角関数では角度はいくらでも大きく、またマイナスの角度も考えられますから。さらに私たちがち2 右図のように ∠ ACB の中に円 ただし, ∠ BOA は図のように,優角(180°よりも大きい角)の方とする 《問題》 次の角度 x , y , z を求め②正多角形のかき方 ③円周率の求め方 (円の円周と直径の関係) ④円周や直径の求め方 ⑤生活の中で円周を求めるよさ 教え方1 正六角形や正八角形を作らせながら、正六角形や正八角形の意味をとらえさせます。 動画を見せて六角形のつくり方を
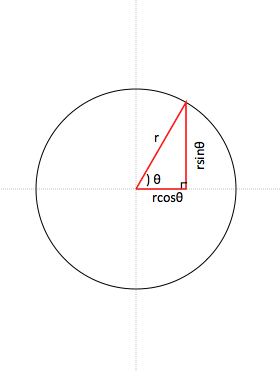
1915 dr リード 円の性質円周角の角度の求め方の3つのパターン下図のように、中心oを通る直線と円との交点をdとします。 円に内接する四角形の対角の和は180°なので ・・・① となります。また1で証明した接弦定理を使うと ・・・② となり、直進の角度は180°なので ・・・③ となります。①、②、③を足せば半径1の円(「単位円」)の円周上の点$(x, y)$がx軸の正方向と角度$\theta$をなすとき、その座標は$(\cos\theta, \sin\theta)$で表されます。 図001 ️三角関数のsinとcos 高校の数学で、三角関数は直角三角形の辺の比で習ったという方も多いでしょう。それはもう忘れて



円の中の角度03 数学教材



円周角の解き方 中学数学に関する質問 勉強質問サイト
②正多角形のかき方 ③円周率の求め方 (円の円周と直径の関係) ④円周や直径の求め方 ⑤生活の中で円周を求めるよさ 教え方1 正六角形や正八角形を作らせながら、正六角形や正八角形の意味をとらえさせます。 動画を見せて六角形のつくり方を円とおうぎ形の公式を覚えれましたか?? 公式がなかなか覚えれないという人の中には 円とおうぎ形の公式を別々に考えている人が多いです。 おうぎ形の公式は 円の公式に\(\times \frac{a}{360}\)をくっつけるだけですからね! 円の公式を覚えてしまえば円が描けてしまえば、図の幾何学的な関係から以下の式を簡単に導くことができます。 まずは円の半径を下式(5224)で求めます。 ・・・(5228) 主応力、主応力方向までの角度θは以下の式で求めることがでいます。



中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット



円周角と孤の比 中学数学に関する質問 勉強質問サイト
半径1の円(「単位円」)の円周上の点$(x, y)$がx軸の正方向と角度$\theta$をなすとき、その座標は$(\cos\theta, \sin\theta)$で表されます。 図001 ️三角関数のsinとcos 高校の数学で、三角関数は直角三角形の辺の比で習ったという方も多いでしょう。それはもう忘れて円とおうぎ形の公式を覚えれましたか?? 公式がなかなか覚えれないという人の中には 円とおうぎ形の公式を別々に考えている人が多いです。 おうぎ形の公式は 円の公式に\(\times \frac{a}{360}\)をくっつけるだけですからね! 円の公式を覚えてしまえば2 右図のように ∠ ACB の中に円 ただし, ∠ BOA は図のように,優角(180°よりも大きい角)の方とする 《問題》 次の角度 x , y , z を求め



ラジアン 弧度法 の意味と 度 への変換方法



中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
円の面積 円の面積と円周の公式はどっちがどっちだか わからなくなることがありますのでしっかり確実に覚えておくようにしましょう。 円の面積 = 半径 × 半径 × 円周率 弧の面積 まず、円の面積を求めて、そのうちの弧の角度分の面積を知りたいの半径1の円(「単位円」)の円周上の点$(x, y)$がx軸の正方向と角度$\theta$をなすとき、その座標は$(\cos\theta, \sin\theta)$で表されます。 図001 ️三角関数のsinとcos 高校の数学で、三角関数は直角三角形の辺の比で習ったという方も多いでしょう。それはもう忘れてランダムに置いた円を回す >> jsdoitへ 円の配置は、中心からの距離と角度をランダムに決めて、第1の方程式で定めました。距離には範囲を定めて、円は中心近くには置かず、真ん中は空白にしています。



扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ
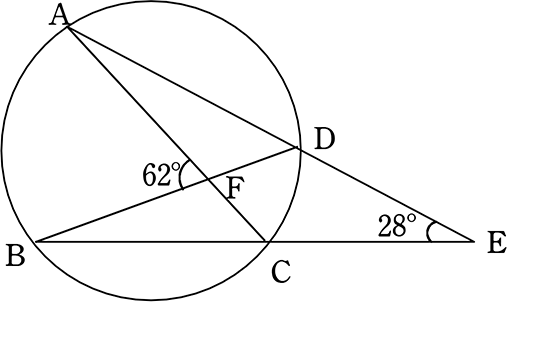


中学数学 円周角 中心角
等速円運動と回転速度 物体が一定の速さで円運動をするとき、この運動のことを等速円運動と言います。 円運動とは、図のように点Oを中心に、AがOの周りを回転運動することでしたね。 物体Aの角速度を「ω」、「OA=r」としたとき、物体Aの回転速度「v
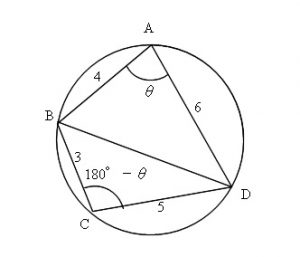


円に内接する四角形の面積の求め方と定理の使い方


角運動の並進速度 接線加速度 求心 向心 加速度の求め方 陸上競技の理論と実践 Sprint Conditioning



角度の求め方 算数の教え上手 学びの場 Com



数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア



75 角度 求め 方 ただぬりえ
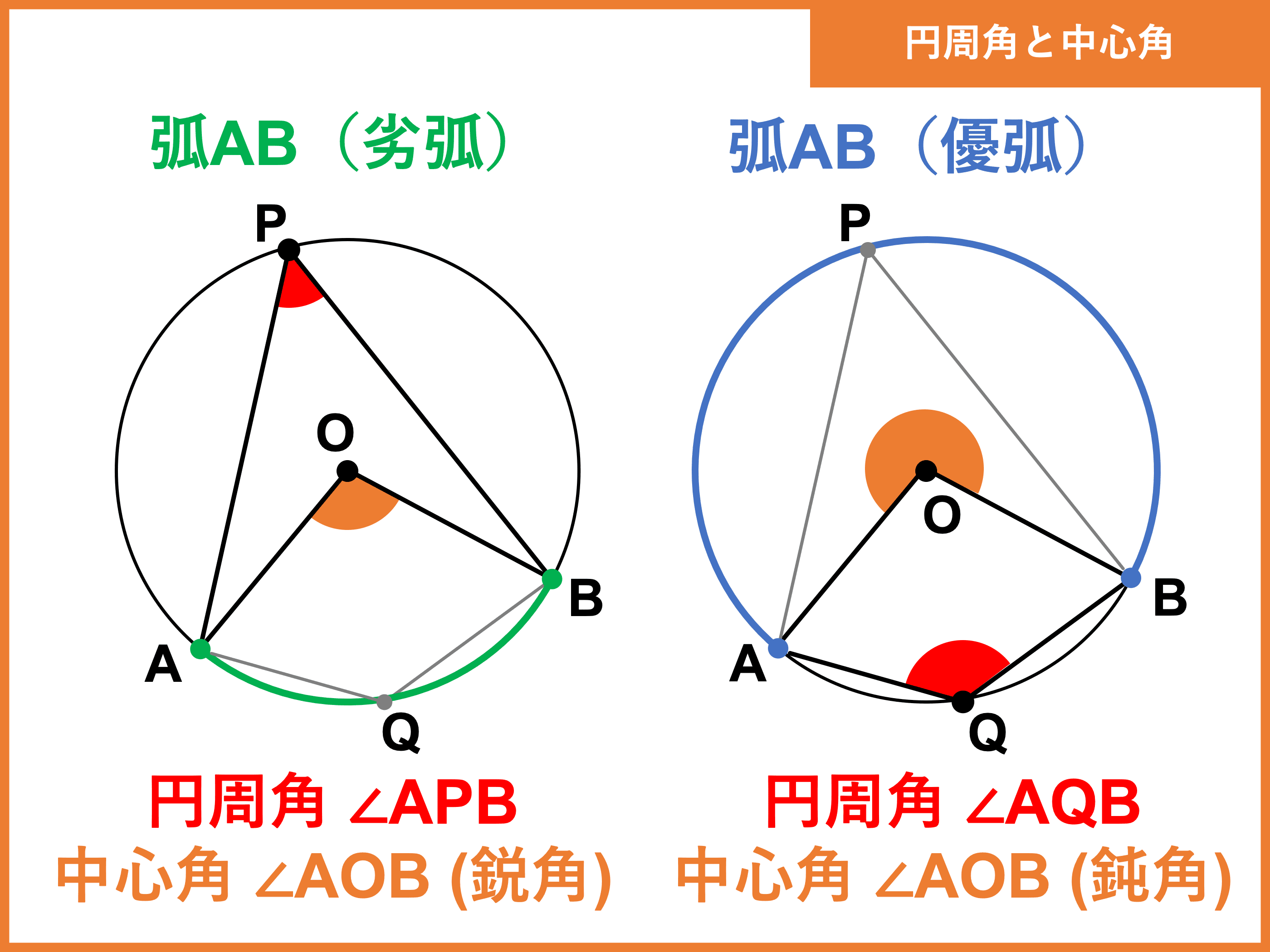


円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典



扇形の弧の長さの求め方 公式と計算例


円周角の定理と中心角 中学3年数学 Youtube


円周角



角度の求め方 算数の教え上手 学びの場 Com



円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
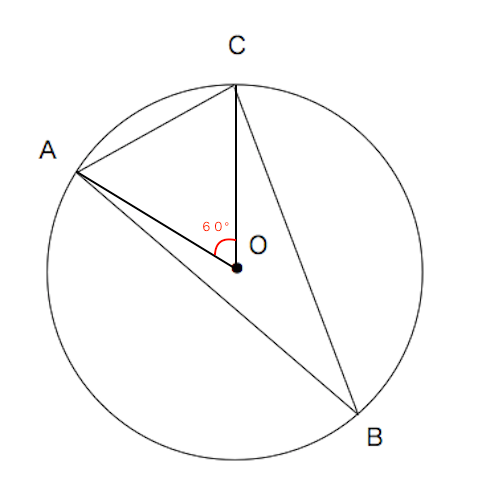


円周角の定理 練習問題 角度がわからない 苦手な数学を簡単に


三角関数の角度は 3分でわかる求め方 公式と計算 表との関係


内接円 内心



中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



円の中の角度02 数学教材



円の中にある二つある三角形の角度の求め方 数学 解決済 教えて Goo



円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ



円周角の定理の基本 計算 無料で使える中学学習プリント
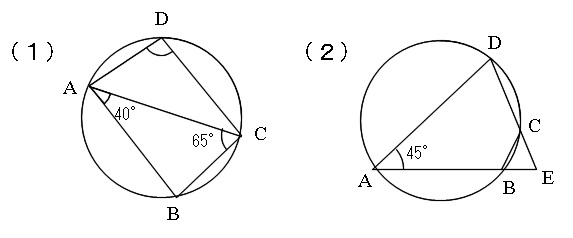


方べきの定理 公式 の覚え方と円に内接する四角形の対角線の性質



1研究中 C 数学2 正弦定理 余弦定理 円周角の定理と外角の定理と四角形の外接円


内接円 内心



三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す
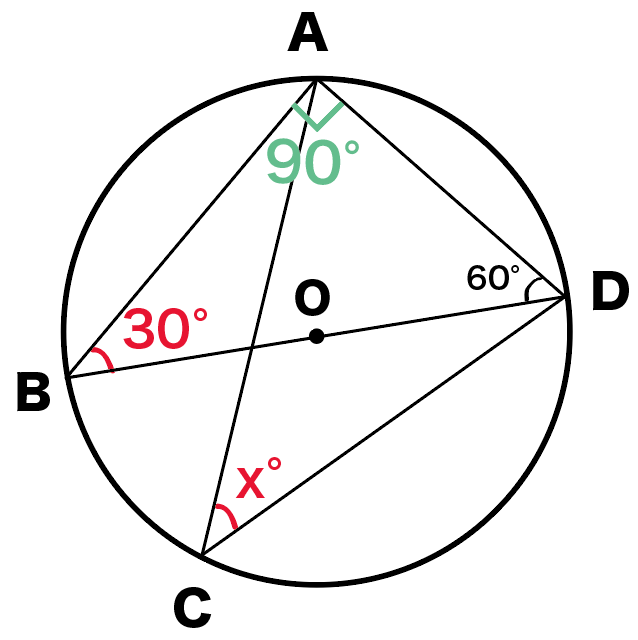


円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
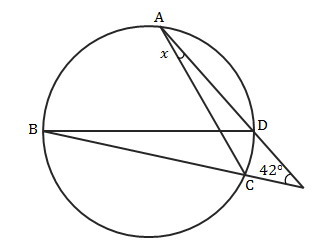


中3数学 円周角 ブーメラン型四角形 まとめと問題



余弦定理で角度を求める方法 数学の星



円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest



Xの角度の求め方を教えて下さい Clear
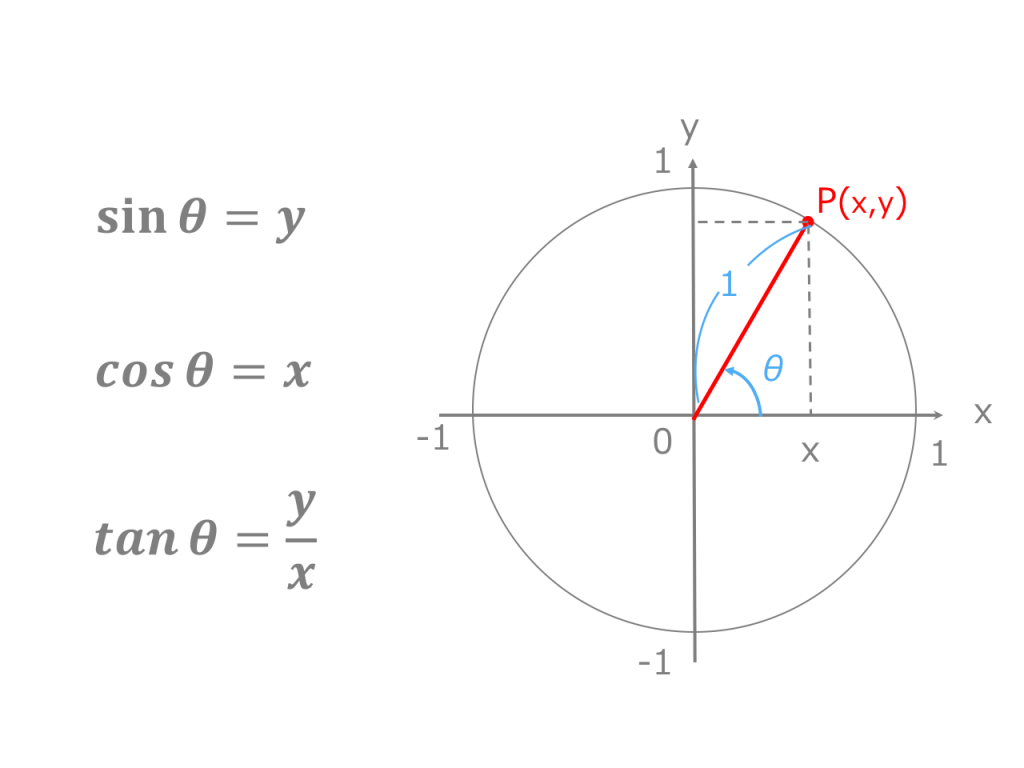


3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ
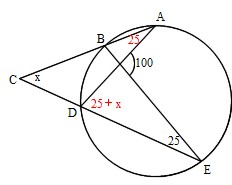


Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ



数学 中3 57 円周角の定理 少し応用編 Youtube
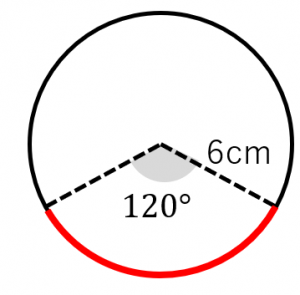


弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学



中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
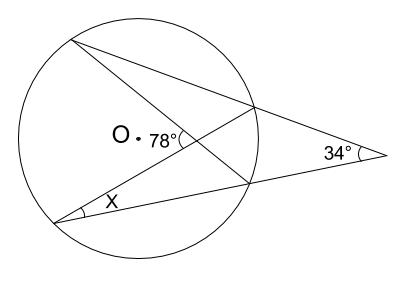


中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



円周角 補助線を引く問題


円の中にある三角形の角度の求め方です 上の円の角oac Adcと下の円の角 Yahoo 知恵袋



円周角の定理 円周角と中心角の関係は中学や高校でよく出るぞ 中学や高校の数学の計算問題



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室
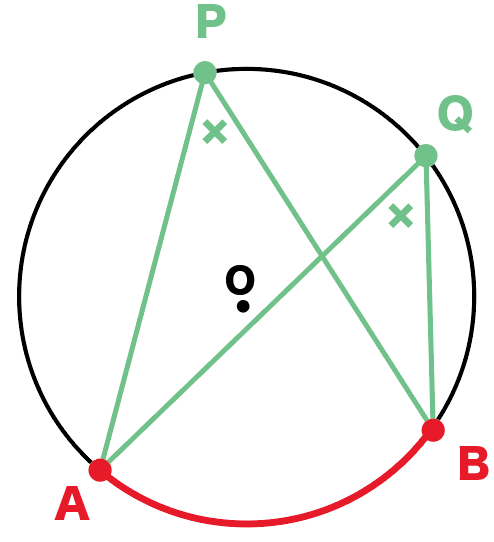


3分でわかる 円周角の定理とはなんだろう Qikeru 学びを楽しくわかりやすく
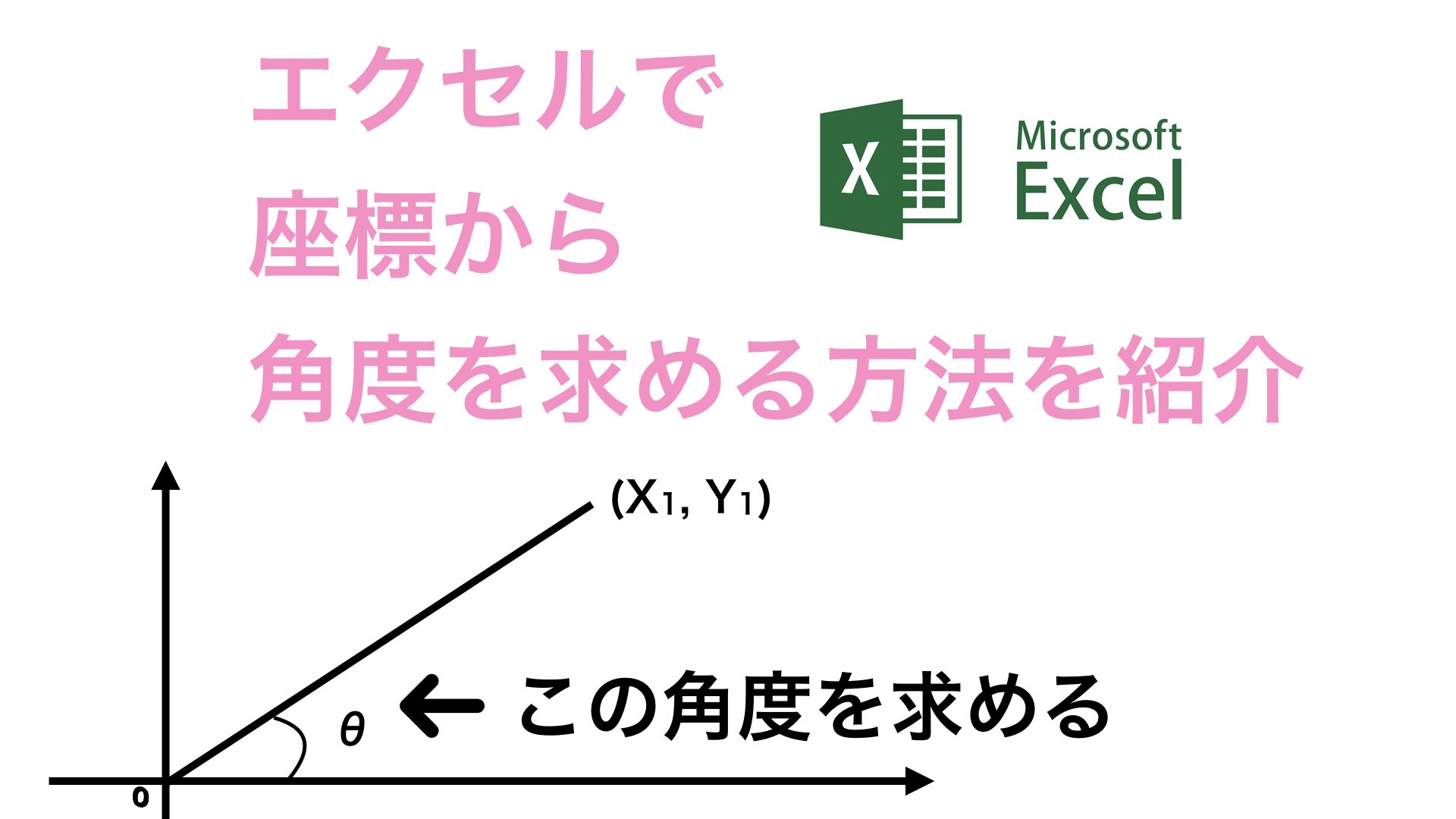


エクセルで座標から角度を求める方法 しおりビルヂング



数学 中3 56 円周角の定理 基本編 Youtube


円周角の定理を使った角度の求め方 写真の問題なんですが適当に書きま Yahoo 知恵袋



数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア


円の中心からの角度から真円の円周上の座標を計算する Gamesprit



開発メモ 円周上の点 自由処



ちょうちょ型図形の角度は 求め方を徹底解説 数スタ



円周率pが現われる世界 3 Pが角度180 ってどういう意味 研究員の眼 ハフポスト
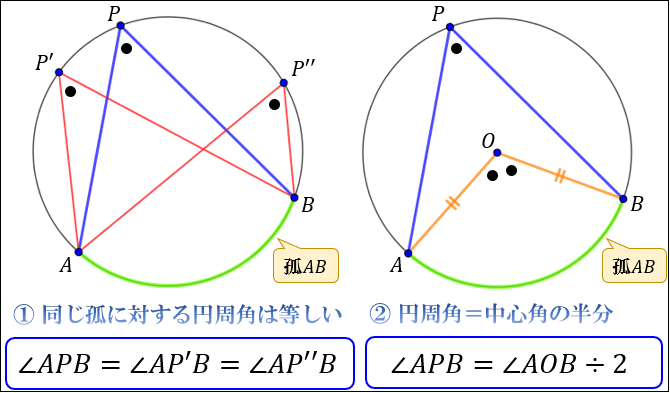


円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ



6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4



中学3年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生



円周角の定理の基本 計算 無料で使える中学学習プリント



内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ



中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名
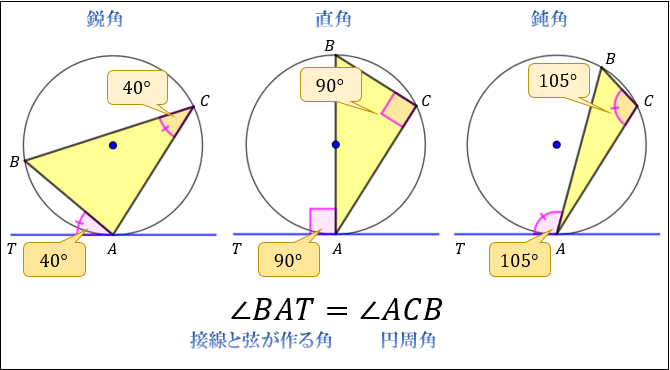


接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



円周角の定理 角度の計算 中学数学 Youtube



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ



中学数学 円周角 中心角



角度を求めよう 円とブーメラン 中学数学 Wiki Atwiki アットウィキ
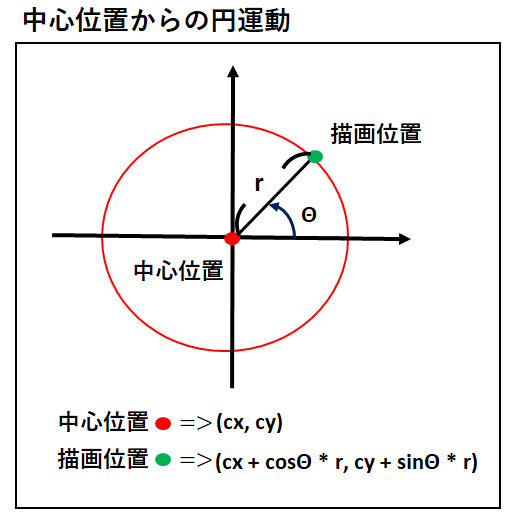


ゲーム 円運動


円と三角形 角度 中学から数学だいすき



円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト



円中の角度 中学数学に関する質問 勉強質問サイト


円周角



円による角度の求め方 中学数学に関する質問 勉強質問サイト


外接円 外心について


中学数学 円周角 中心角



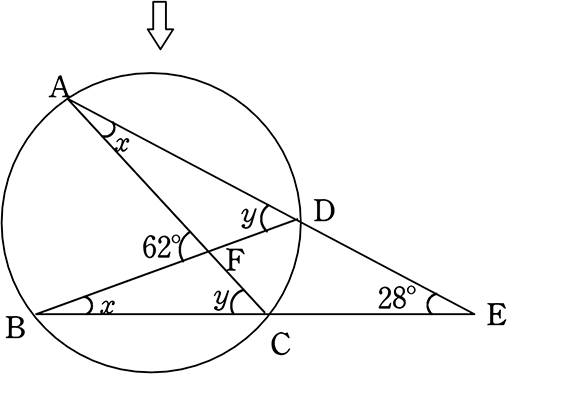
平面図形 円の中にある三角形の角度を求めるには 早稲田中学校の入試問題から 親子で挑戦 中学受験算数 朝日新聞edua
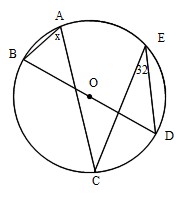


Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ



おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook



接線と円の関係 Jsciencer
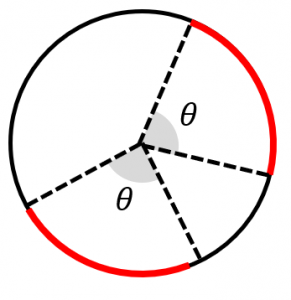


弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学



中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット


プチコン講座 角度計算の基本 ラジアン 三角関数
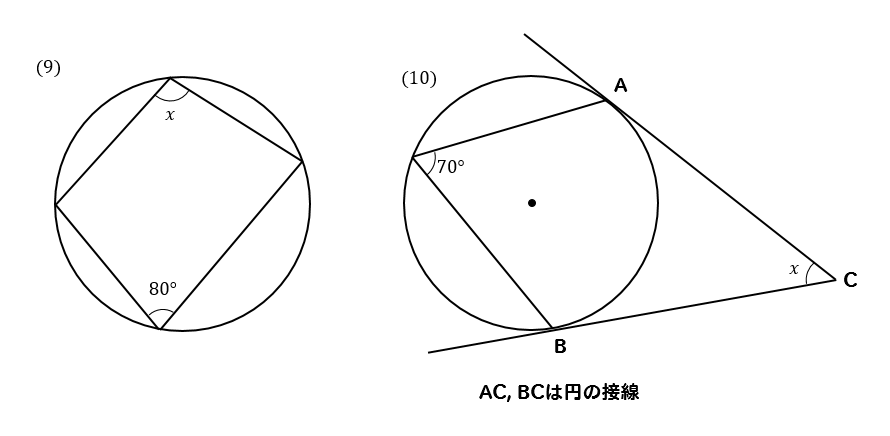


これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ
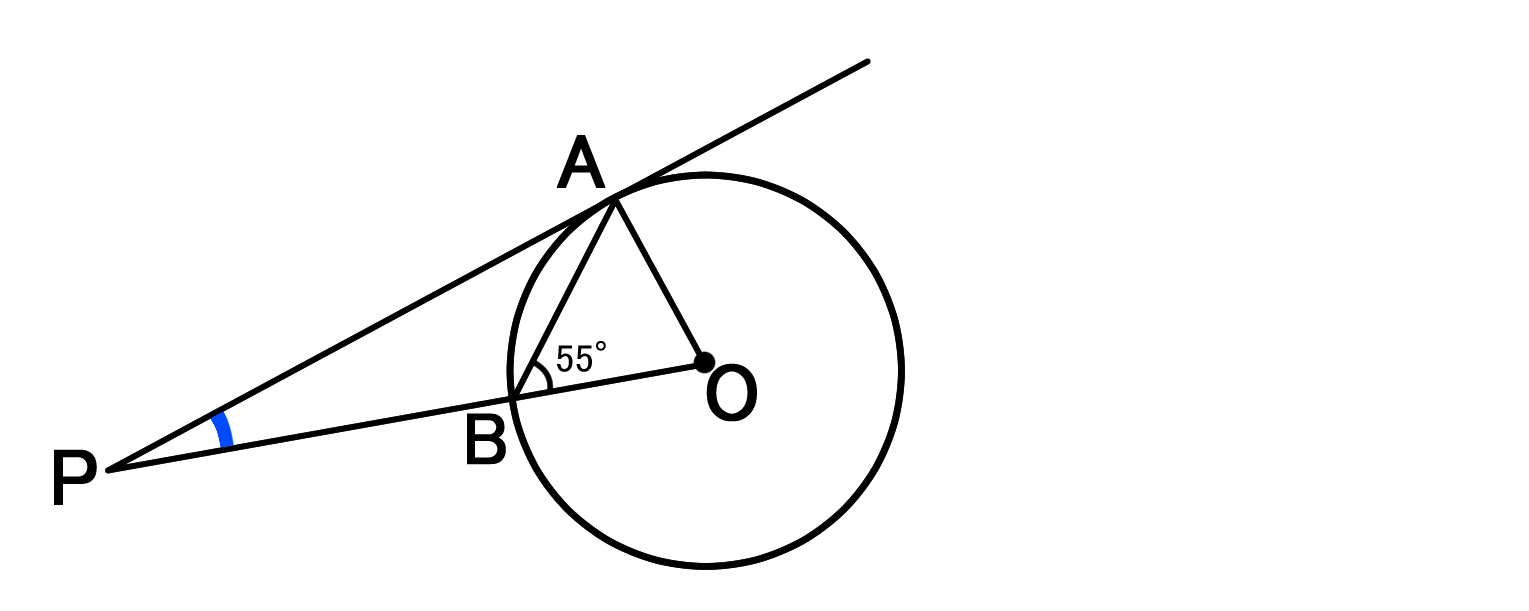


円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学
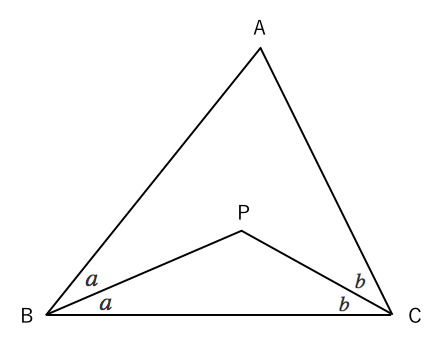


図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に



余弦定理の証明とは 角度 面積を求める計算問題や公式の覚え方をわかりやすく解説 遊ぶ数学
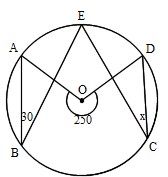


Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ
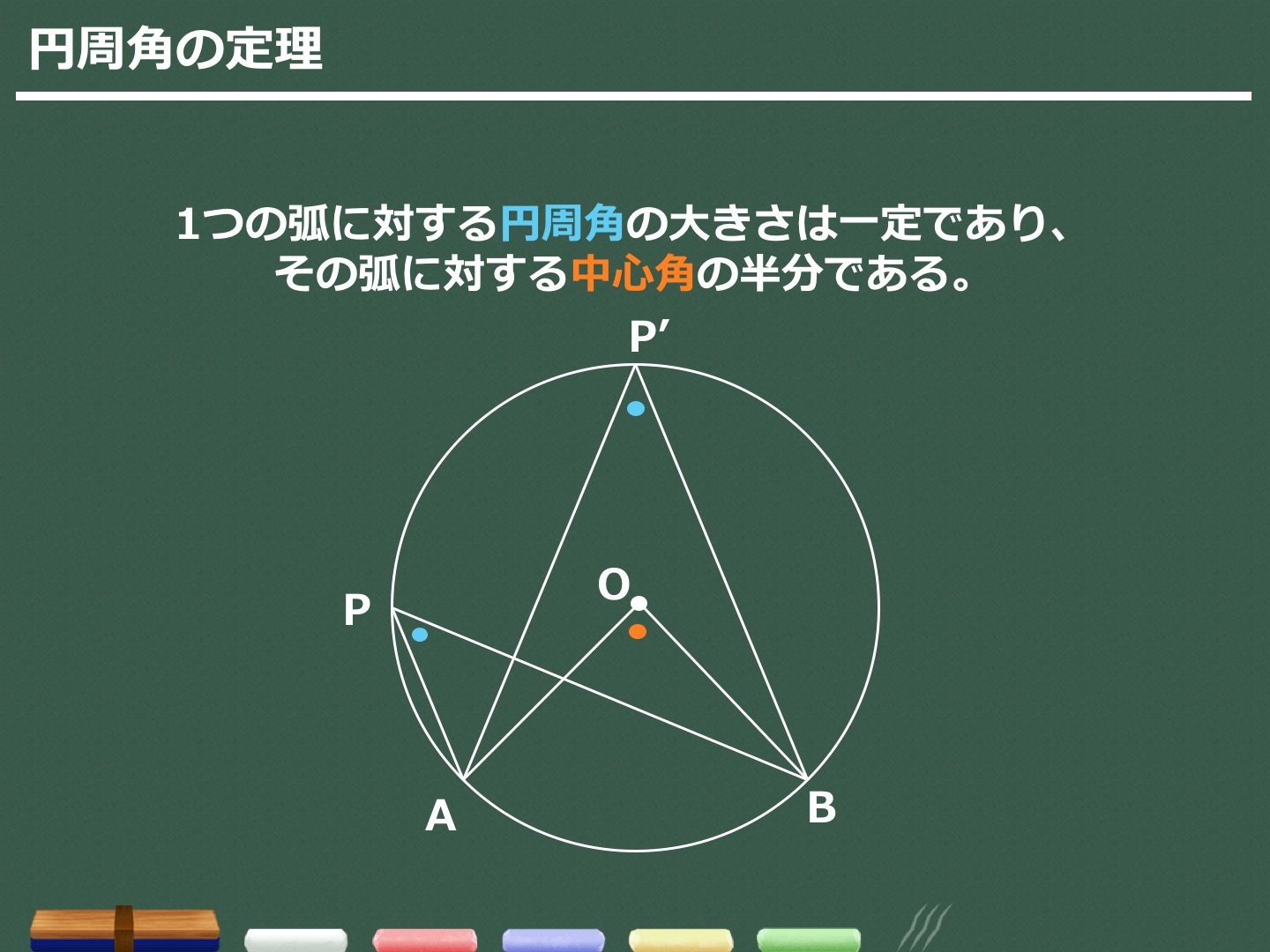


3分でわかる 円周角の定理とその逆の証明 問題の解き方 合格サプリ


三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典


円の接線と角度 中学から数学だいすき



円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ



三角関数で角度から座標を導くふたつの式の使い途 Qiita



三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ


円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



角度の求め方を教えてください ちなみに答えは です お願いします Clear


円と三角形 角度 中学から数学だいすき



円周角の定理の基本 計算 無料で使える中学学習プリント
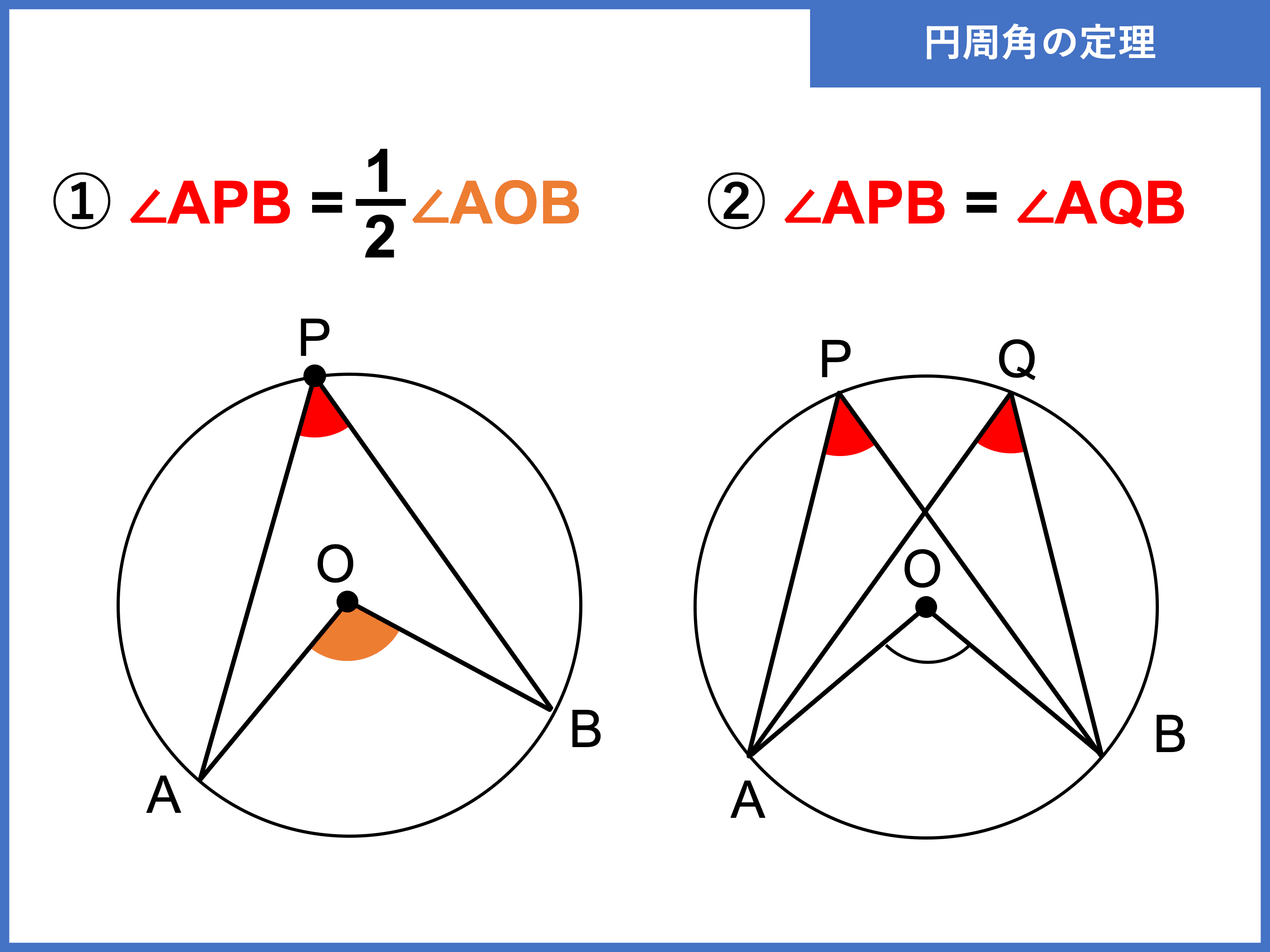


円周角の定理とは 定理の逆や証明 問題の解き方 受験辞典


